チェビシェフ・フィルタの設計原理をやさしく解説

チェビシェフ・フィルタとは

通過域の振幅特性にリップル (小さな凸凹) を許す代わりに、カットオフが急峻で阻止域の減衰を大きくとれるフィルタです。

チェビシェフ LPF/BPF/HPF を設計できる無料オンライン・ツールはこちら ⇒

基準ロー・パス・フィルタの考え方

フィルタ設計は、カットオフ角周波数 \(\omega_c=1\) の基準ロー・パス・フィルタ(LPF)を作ることから始まります。

図 1 のように \(\omega\) が 0～1 の範囲では 0 に近く、\(\omega\) が 1 を超えると急に大きくなる関数 \(f(\omega)\) があるとします。

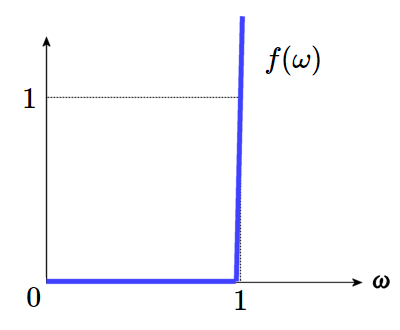
この \(f(\omega)\) を使って \(g(\omega)=\displaystyle\frac{1}{1+f(\omega)}\) を作れば、図 2 に近い形になるでしょう。
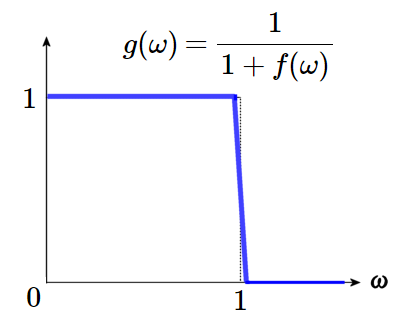
これはカットオフ角周波数が \(\omega=1\) の基準ロー・パス・フィルタ (LPF) 特性そのものです。

チェビシェフ多項式

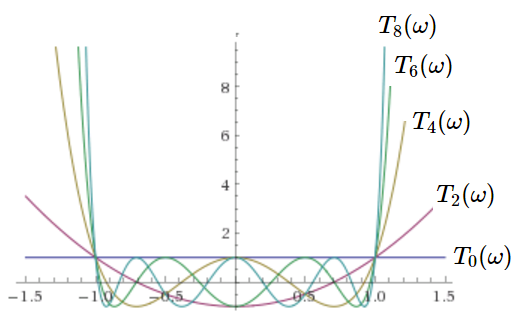
チェビシェフ・フィルタは \(f(\omega)\) に以下の第1種チェビシェフ多項式 \(T_n(\omega)\) を用いたものです。 \begin{eqnarray} T_0(\omega) &=& 1 \label{T0}\\ T_1(\omega) &=& \omega \\ T_2(\omega) &=& 2 \omega^2-1 \\ T_3(\omega) &=& 4 \omega^3-3 \omega \\ T_4(\omega) &=& 8 \omega^4 - 8 \omega^2 + 1 \\ T_5(\omega) &=& 16 \omega^5 - 20 \omega^3 + 5 \omega \\ T_6(\omega) &=& 32 \omega^6 - 48 \omega^4 + 18 \omega^2 -1 \\ T_7(\omega) &=& 64 \omega^7 - 112 \omega^5 + 56 \omega^3 -7 \omega \\ T_8(\omega) &=& 128 \omega^8 - 256 \omega^6 + 160 \omega^4 - 32 \omega^2 + 1 \label{T8}\\ &\vdots& \nonumber \end{eqnarray} グラフを描くと次のような形をしています。

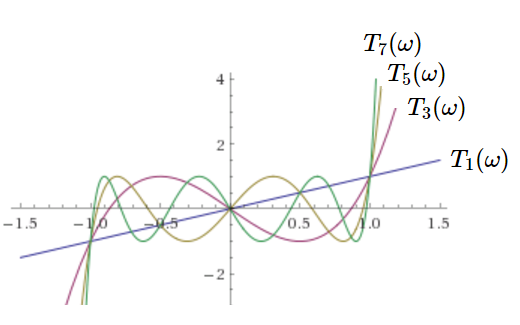
\(T_n(\omega)\) は \(|\omega|\leq 1\) の範囲では \(\cos\) の \(n\) 倍角公式を与える多項式でもあります。 \begin{eqnarray} T_n(\omega) &=& \cos(n \cos^{-1}\omega) \label{Tw} \end{eqnarray}

設計法

振幅2乗特性を定義する

\(T_n(\omega)\) を使って次のようにフィルタの振幅2乗特性を定義します。 \begin{eqnarray} |H(\omega)|^2 &=& \frac{1}{1+\varepsilon^2T_n^2(\omega)} \label{Hw} \end{eqnarray} \(\varepsilon\) は通過域のリップルを決める \(0 < \varepsilon < 1\) のパラメータです。

　　\(f(\omega)=\varepsilon T_n(\omega)\) でなく \(f(\omega)=\varepsilon^2 T_n^2(\omega)\) と 2 乗して、分母多項式を \(2n\) 次にしておくところがポイントです。

極の分布を調べる

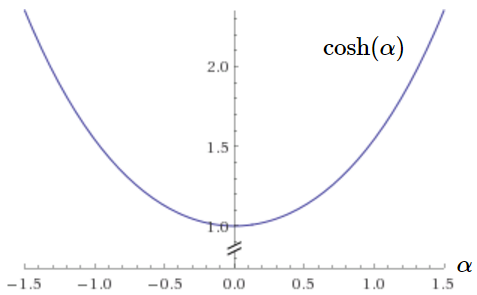
\(s\) 平面の虚軸上で式(\ref{Hw}) が成り立つなら \begin{eqnarray} |H(\omega)|^2 &=& \frac{1}{1+\varepsilon^2T_n^2(\omega)} \\ && 虚軸\ s=i\omega\ 上では\ \omega=\frac{1}{i}s=-is \ だから \nonumber\\ &=& \frac{1}{1+\varepsilon^2T_n^2(-is)} \label{Hw2} \end{eqnarray} と表せますが、しばらくはフィルタの極についてだけ考えましょう。極は式(\ref{Hw2})の分母が 0 になる所ですから \begin{eqnarray} 1+\varepsilon^2T_n^2(-is) &=& 0 \\ && 移項して \\ \varepsilon^2T_n^2(-is) &=& -1 \\ && 両辺を \varepsilon^2 で割って \\ T_n^2(-is) &=& -\frac{1}{\varepsilon^2} \\ && 平方根を取ると \sqrt{-1}=i だから \\ T_n(-is) &=& \pm\frac{i}{\varepsilon} \label{Tis} \end{eqnarray} ですが、一方、式(\ref{Tw})に \(\omega=-is\) を代入すると次式も成り立ちます。 \begin{eqnarray} T_n(-is) &=& \cos\{n \cos^{-1}(-is)\} \label{Tnis} \end{eqnarray} 式(\ref{Tis})と式(\ref{Tnis})は等しいので、\(s\) が極なら次式を満たさねばなりません。 \begin{eqnarray} \pm\frac{i}{\varepsilon} &=& \cos\{n \cos^{-1}(-is)\} \label{iecos} \end{eqnarray} ここで \begin{eqnarray} \cos^{-1}(-is)=x+iy \label{xiy} \end{eqnarray} と置くと、式(\ref{iecos})は次のように書けます。 \begin{eqnarray} \pm\frac{i}{\varepsilon} &=& \cos(nx+iny) \\ && 三角関数の加法定理より \nonumber\\ &=& \cos(nx)\cos(iny)-\sin(nx)\sin(iny) \\ && ここで \cos(i\alpha)=\cosh(\alpha),\ \sin(i\alpha)=i\sinh(\alpha)\ と書けるので \nonumber\\ &=& \underbrace{\cos(nx)\cosh(ny)}_{実部}-i\ \underbrace{\sin(nx)\sinh(ny)}_{虚部} \label{ie} \end{eqnarray} 左辺は純虚数ですので、式(\ref{ie})右辺第1項(実部)は 0 でなければなりませんから、 \begin{eqnarray} \cos(nx)\cosh(ny)=0 \label{coscosh} \end{eqnarray} 下の図 5 から判るように \(\cosh(\alpha)>0\) ですから、式(\ref{coscosh}) が 0 になるには \(\cos(nx)=0\) が必要で、\(x\) は \begin{eqnarray} nx=\displaystyle\frac{\pi}{2}+m\pi,\ m=0,\pm 1,\pm 2,\cdots \label{nx} \end{eqnarray} を満たさねばなりません。両辺を \(n\) で割って \begin{eqnarray} x &=& \frac{\pi}{2n}+\frac{m\pi}{n} = \frac{2m+1}{2n}\pi \label{x} \end{eqnarray} を得ます。

また、式(\ref{ie})右辺第1項は 0 ですので、第2項が左辺に等しくなければなりません。 \begin{eqnarray} -i\sin(nx)\sinh(ny) &=& \pm\frac{i}{\varepsilon} \end{eqnarray} 式(\ref{nx})より \(\sin(nx)=\pm1\) ですから、両辺を \(-i\) で割って複号の順序を無視すれば、次のように書けます。 \begin{eqnarray} \sinh(ny) &=& \pm\frac{1}{\varepsilon} \end{eqnarray} これを \( y \) について解くと、次のようになります。 \begin{eqnarray} y &=& \pm\frac{1}{n}\sinh^{-1}{\frac{1}{\varepsilon}} \label{y} \end{eqnarray} 式(\ref{xiy})から \begin{eqnarray} -is &=& \cos(x+iy) \end{eqnarray} であり、フィルタの極は両辺を \(-i\) で割って \begin{eqnarray} s &=& i\cos(x+iy) \\ && 三角関数の加法定理より \nonumber\\ &=& i\{\cos(x)\cos(iy)-\sin(x)\sin(iy)\} \\ && ここで \cos(i\alpha)=\cosh(\alpha),\ \sin(i\alpha)=i\sinh(\alpha)\ と書けるので \nonumber\\ &=& i\{\cos(x)\cosh(y)-i\sin(x)\sinh(y)\} \\ &=& \sin(x)\sinh(y) + i\ \cos(x)\cosh(y) \end{eqnarray} にあることがわかります。以下、極 (pole) を \(p\) と書くことにします。 \begin{eqnarray} p &=& \underbrace{\sin(x)\sinh(y)}_{実部} + i\ \underbrace{\cos(x)\cosh(y)}_{虚部} \label{p} \end{eqnarray} 式(\ref{x})と式(\ref{y})をひとまとめにすると \begin{eqnarray} \left\{ \begin{array}{ll} x = \displaystyle\frac{2m+1}{2n}\pi,& \ m=0,\pm 1,\pm 2,\cdots \\ y = \pm\displaystyle\frac{1}{n}\sinh^{-1}{\frac{1}{\varepsilon}} \end{array} \right. \end{eqnarray} ですので、この \(x,y\) を式(\ref{p})に入れて、実際に極 \(p\) が s 平面でどのように分布しているのか見てみましょう。

下図6 は 6次チェビシェフ・フィルタで \(\varepsilon=0.5\) とした時の極の分布、下図7 はフィルタの次数を 7 次にした場合の極の分布です (赤い × 印が極)。



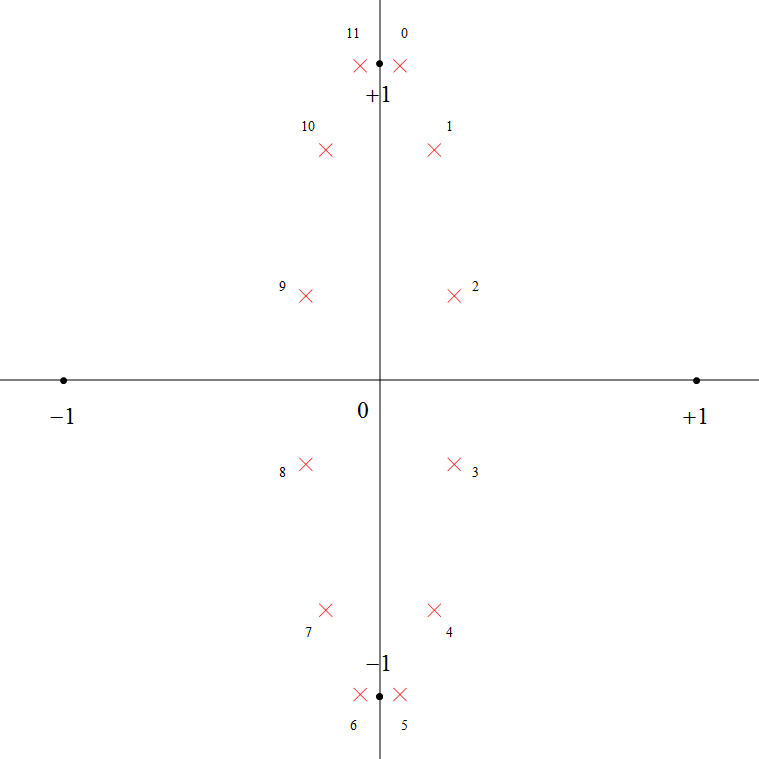
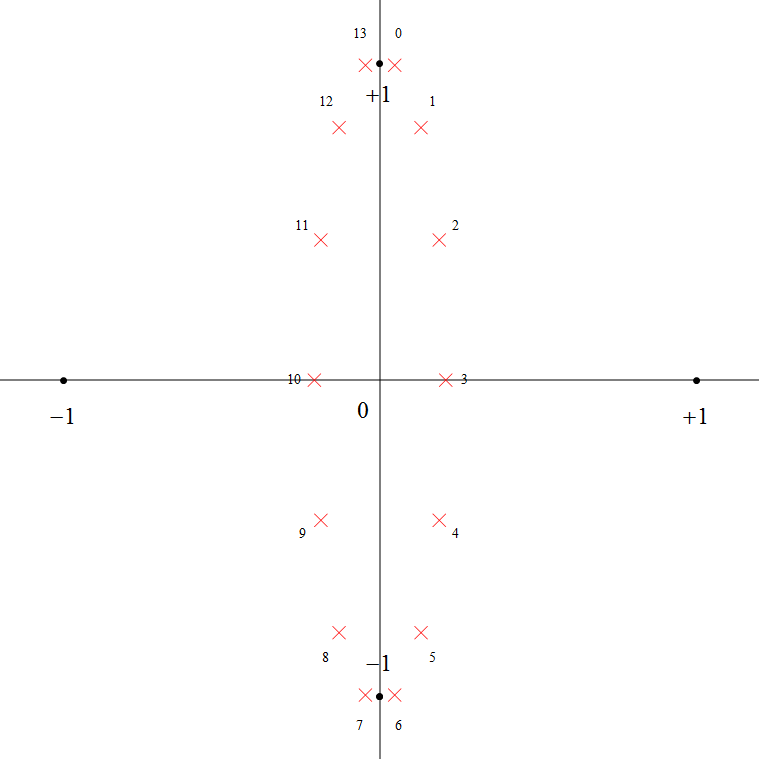
図から判るように極 \(p\) は、s 平面の実軸と虚軸に対して対称な潰れた楕円のような形に分布しており、奇数次の場合は実軸上に極を持ちます。

不安定な極を取り除く

s 平面の右半平面に極があるため、このままではフィルタが不安定になってしまいますので、左半平面の極だけを残して右半平面の極を全て捨て、図8,9 のようにします。

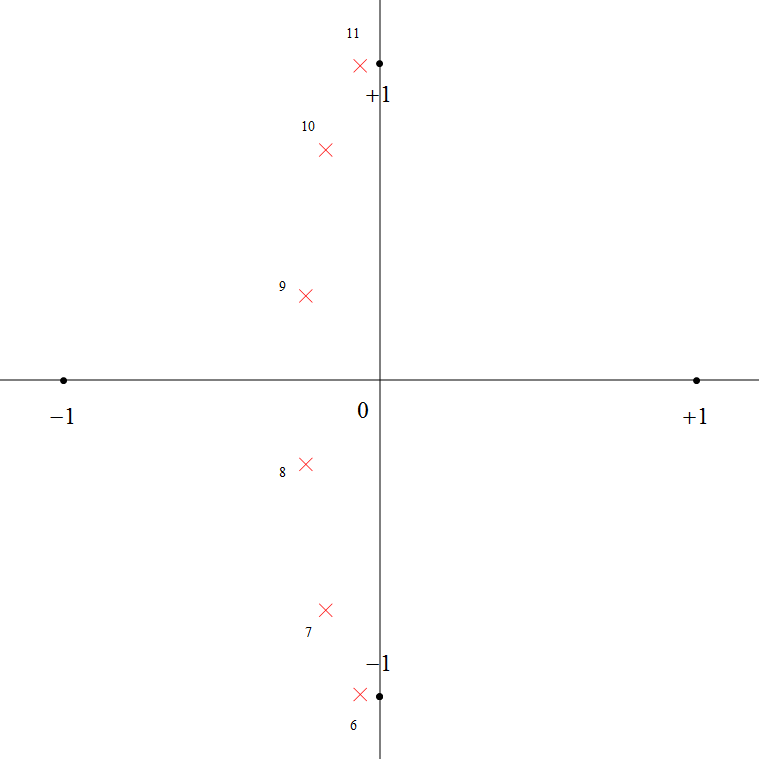
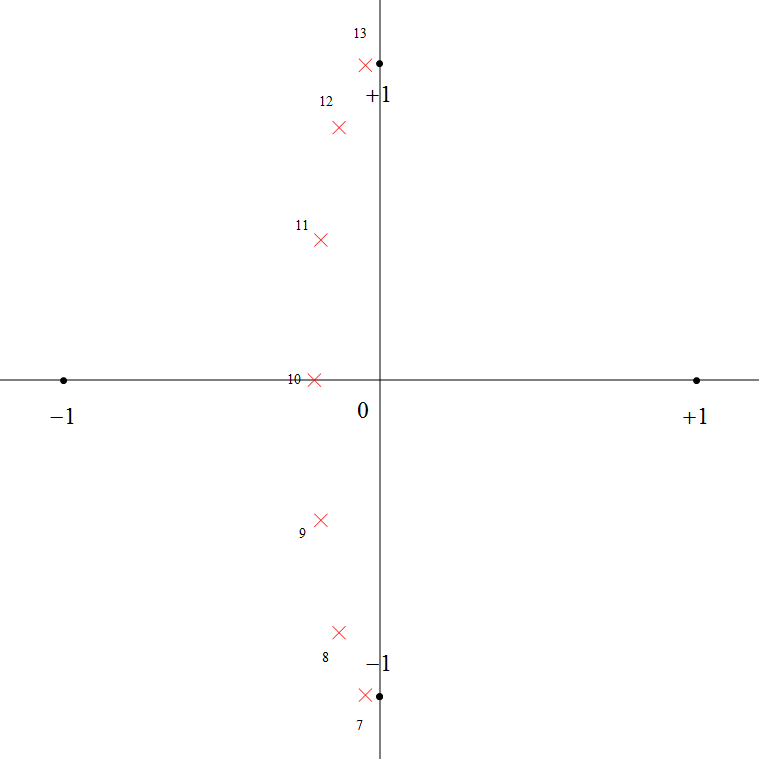
こうするとフィルタ次数は \(2n\) 次から \(n\) 次に半減し、阻止域の減衰量はデシベルで半分になってしまいますが、安定なフィルタを得ることができます。

先程「分母多項式を \(2n\) 次にしておくところがポイント」と書いたのは、「後で極を半分捨てることになるので、あらかじめ極の個数を倍にしておく」ということだったのです。

1次,2次フィルタに分解する

奇数次の場合、極のひとつは実軸上にあり、虚部は 0 ですから、次のように書けます。 \begin{eqnarray} p &=& \sin(x)\sinh(y) \end{eqnarray} この極を持つ 1 次フィルタは次のようになります。 \begin{eqnarray} F_1(s) &=& \frac{1}{s-p} \label{F1} \end{eqnarray} それ以外の場合は、\(p\) が極なら複素共役な極 \(p^*\) もペアで存在しています(そうでないとインパルス応答が実数値になりません)から \begin{eqnarray} p,p^* &=& \sin(x)\sinh(y) \pm i\cos(x)\cosh(y) \label{ppstar} \end{eqnarray} \(p\) と \(p^*\) をセットにしてひとつの 2 次フィルタとすれば、次のようになります。 \begin{eqnarray} F_2(s) &=& \frac{1}{(s-p)(s-p^*)} \\ &=& \frac{1}{s^2-(p+p^*)s+pp^*} \\ &=& \frac{1}{s^2-2Re[p]s+|p|^2} \label{F2} \end{eqnarray} \(Re[p]\) は式(\ref{ppstar})の実部ですので、簡単に求められます。 \begin{eqnarray} Re[p] &=& \sin(x)\sinh(y) \end{eqnarray} \(|p|^2\) は \begin{eqnarray} |p|^2 &=& \sin^2(x)\sinh^2(y) + \cos^2(x)\cosh^2(y) \end{eqnarray} ですが、sin,cos,sinh,cosh を指数関数表示して、もう一手間かければ \begin{eqnarray} |p|^2 &=& \left(\frac{e^{ix}-e^{-ix}}{2i}\right)^2 \left(\frac{e^{x}-e^{-x}}{2}\right)^2 + \left(\frac{e^{ix}+e^{-ix}}{2}\right)^2 \left(\frac{e^{x}+e^{-x}}{2}\right)^2 \\ &=& \frac{1}{4}\left(e^{2 x} + e^{-2 x} + e^{2 i x} + e^{-2 i x}\right) \\ &=& \frac{1}{2}\left(\cos 2x + \cosh 2y\right) \end{eqnarray} と簡単化できます。

ゲインを調整する

得られた極に対応する式(\ref{F1}), 式(\ref{F2}) のフィルタをいくつか直列接続すればロー・パス・フィルタにはなりますが、極を決めただけでは通過域のゲインが希望値になりません。

ゲインの設計法

振幅2乗特性を表す式(\ref{Hw2})から \begin{eqnarray} |H(\omega)|^2 &=& \frac{1}{1+\varepsilon^2T_n^2(-is)} \nonumber \\ && T_n(\omega) は最高次の係数が 2^{n-1} なので \nonumber \\ &=& \frac{1}{1+\varepsilon^2 \left\{2^{n-1}(-is)^n + \cdots \right\}^2} \\ &=& \frac{1}{\varepsilon^2 2^{2(n-1)}(-i)^{2n} \left(s^n + \cdots \right)^2+1} \\ &=& \frac{1}{\varepsilon^2 2^{2(n-1)}(-1)^n \left(s^n + \cdots \right)^2+1} \\ && 最高次の係数を \pm 1 にするため、分母子を \varepsilon^2 2^{2(n-1)} で割って展開して \nonumber\\ &=& \frac{\varepsilon^{-2} 2^{-2(n-1)}}{(-1)^n \left(s^{2n} + \cdots \right)} \\ && m 番目の極を p_m で表し、分子を整理すると \nonumber\\ &=& \frac{(2^{1-n}/\varepsilon)^2}{(-1)^n \displaystyle\prod_m \left(s-p_m\right)} \end{eqnarray} ですので、希望の特性を得るにはゲイン \(2^{1-n}/\varepsilon\) を掛ける必要があります (ゲインは振幅2乗特性の平方根なので、 \((2^{1-n}/\varepsilon)^2\) ではなく \(2^{1-n}/\varepsilon\) を掛けます)。

\(\varepsilon\) の設計法

図3, 図4 から判るようにチェビシェフ多項式は次数 \(n\) に関係なく \(T_n(1)=1\) ですので、式(\ref{Hw})から \(\omega=1\) での振幅2乗特性は \begin{eqnarray} |H(1)|^2 &=& \frac{1}{1+\varepsilon^2T_n^2(1)}\ =\ \frac{1}{1+\varepsilon^2} \end{eqnarray} となり、ここでリップルが \(-r\) dB になるには \begin{eqnarray} 10\log_{10}\frac{1}{1+\varepsilon^2} &=& -r \end{eqnarray} とすればよく、\(10\log_{10}\) を外して \begin{eqnarray} \frac{1}{1+\varepsilon^2} &=& 10^{-r/10} \end{eqnarray} 逆数を取って \begin{eqnarray} 1+\varepsilon^2 &=& \frac{1}{10^{-r/10}}\ =\ 10^{r/10} \\ \end{eqnarray} 両辺から 1 を引いて平方根を取り \begin{eqnarray} \varepsilon &=& \sqrt{10^{r/10}-1} \label{eps} \end{eqnarray} とすれば \(\omega=1\) で \(-r\) dB のリップルを持つチェビシェフ・フィルタを作れます。

設計例

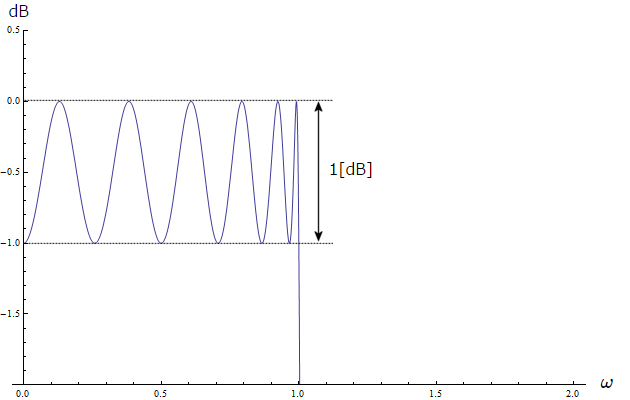
通過域で 1dB のリップルを持つ 12 次 (\(n=12\)) のチェビシェフ基準 LPF を設計してみましょう。
リップルは 1dB ですので式(\ref{eps}) に \(r=1\) を代入して \begin{eqnarray} \varepsilon &=& \sqrt{10^{1/10}-1} \simeq 0.50884713991 \end{eqnarray} とすれば設計できます。
下に設計されたフィルタの振幅特性を示します (横軸はリニアの \(\omega\)、縦軸は dB です)。

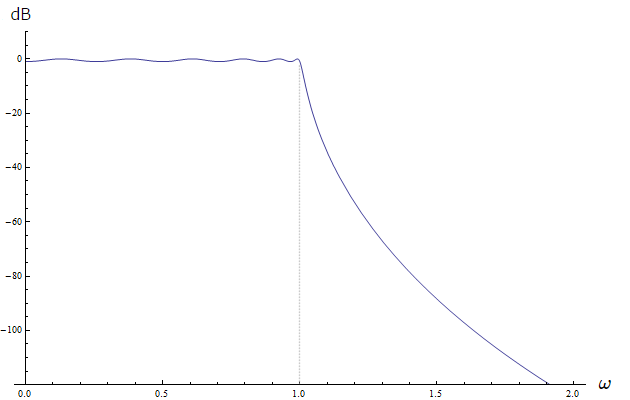
振幅特性はカットオフ角周波数 \(\omega=1\) を過ぎると急角度で減衰し、オクターブ上の \(\omega=2\) では 120dB 以上減衰しています。

通過域を拡大してみると、設計どおり 1dB のリップルを生じています。