へ

平均 (へいきん)

普通、「平均」と言った場合は 算術平均 を意味する。 \begin{eqnarray} a = \frac{1}{N}\sum_{n=0}^{N-1} x_n &=& \frac{x_0 + x_1 + x_2 + \cdots + x_{N-1}}{N} \end{eqnarray}

ベクトル積 (べくとるせき)

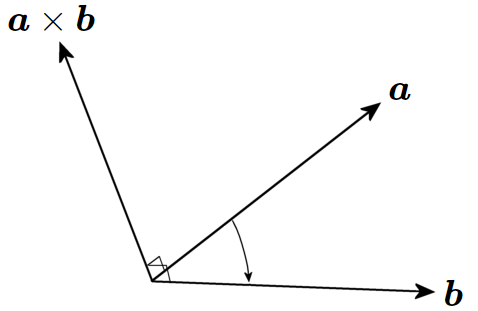
2 つの 3 次元ベクトル $\boldsymbol{a}=(a_x,a_y,a_z)^\top, \boldsymbol{b}=(b_x,b_y,b_z)^\top$ に対して \begin{eqnarray} \boldsymbol{a}\times \boldsymbol{b} &\triangleq& \left| \begin{array}{ccc} \boldsymbol{i} & \boldsymbol{j} & \boldsymbol{k} \\ a_x & a_y & a_z \\ b_x & b_y & b_z \end{array} \right| \\ &=& \left| \begin{array}{cc} a_y & a_z \\ b_y & b_z \end{array} \right| \boldsymbol{i} - \left| \begin{array}{cc} a_x & a_z \\ b_x & b_z \end{array} \right| \boldsymbol{j} + \left| \begin{array}{cc} a_y & a_z \\ b_y & b_z \end{array} \right| \boldsymbol{k} \\ &=& (a_y b_z-a_z b_y)\boldsymbol{i} - (a_x b_z-a_z b_x)\boldsymbol{j} + (a_x b_y-a_y b_x)\boldsymbol{k} \\ &=& (a_y b_z-a_z b_y,\ a_z b_x-a_x b_z,\ a_x b_y-a_y b_x)^\top \end{eqnarray} をベクトル積と呼ぶ。

$\boldsymbol{a}\times \boldsymbol{b}$ は、右ネジを $\boldsymbol{a}$ から $\boldsymbol{b}$ へ回転させた時に、ネジが進む方向を向く。

ヘッセ行列 (へっせぎょうれつ)

以下の行列を $\boldsymbol{x}=(x_0,x_1,\cdots x_{N-1})^\top$ における関数 $f(\boldsymbol{x})$ のヘッセ行列またはヘッシアン(ヘシアンとも)という。 \begin{eqnarray} \boldsymbol{H}(\boldsymbol{x}) &=& \left( \begin{array}{cccc} \frac{\partial^2}{\partial x_0^2} f(\boldsymbol{x}) & \frac{\partial^2}{\partial x_0 \partial x_1} f(\boldsymbol{x}) & \cdots & \frac{\partial^2}{\partial x_0 \partial x_{N-1}} f(\boldsymbol{x}) \\ \frac{\partial^2}{\partial x_1 \partial x_0} f(\boldsymbol{x}) & \frac{\partial^2}{\partial x_1^2} f(\boldsymbol{x}) & \cdots & \frac{\partial^2}{\partial x_1 \partial x_{N-1}} f(\boldsymbol{x}) \\ \vdots && \ddots & \vdots \\ \frac{\partial^2}{\partial x_{N-1}^2} f(\boldsymbol{x}) & \frac{\partial^2}{\partial x_{N-1} \partial x_1} f(\boldsymbol{x}) & \cdots & \frac{\partial^2}{\partial x_{N-1} \partial x_{N-1}} f(\boldsymbol{x}) \\ \end{array} \right) \end{eqnarray} ヘッセ行列が停留点で正値対称行列なら $f(\boldsymbol{x})$ はそこで極小となり、負値対称行列なら $f(\boldsymbol{x})$ はそこで極大となる。

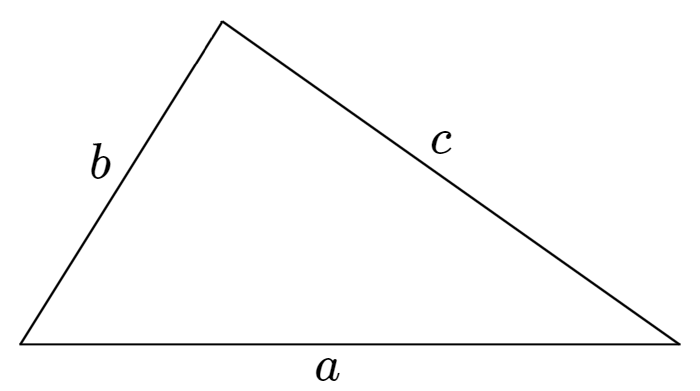
ヘロンの公式 (へろんのこうしき)

ヘロン (Heron) の公式は、各辺の長さが $a,b,c$ の3角形の面積は \begin{eqnarray} s &=& \frac{a+b+c}{2} \label{s} \end{eqnarray} を用いて \begin{eqnarray} S &=& \sqrt{s(s-a)(s-b)(s-c)}, \end{eqnarray} で計算できるという幾何学の定理。