サンプリング・データに直線を当てはめる

概要

ディジタル信号処理では、時刻が \(n=0,1,2,\cdots\) と 0 から始まる連続した整数で表されますので、サンプリング・データ \(y(n),\ n=0,1,\cdots N-1\) に直線 \begin{eqnarray} f(n) &=& a n+b \label{f0} \end{eqnarray} を当てはめるのは、連立1次方程式を解かねばならない \(\{x(n),y(n)\}\) に対する直線当てはめ(直線回帰)より、ずっと簡単にできます。

計算原理

最小2乗法で計算します。当てはめ誤差を \begin{eqnarray} \varepsilon &=& \sum_{n=0}^{N-1} \left\{f(n)-y(n)\right\}^2 \end{eqnarray} で評価すると、\(\varepsilon\) が最小になる \(a,b\) は \begin{eqnarray} \frac{\partial}{\partial a}\varepsilon &=& \frac{\partial}{\partial a} \sum_{n=0}^{N-1} \left\{f(n)-y(n)\right\}^2 \\ &=& 2 \sum_{n=0}^{N-1} \left\{f(n)-y(n)\right\} \frac{\partial}{\partial a} f(n) \\ && 式(\ref{f0}) より \frac{\partial}{\partial a} f(n)=n\ だから \nonumber\\ &=& 2 \sum_{n=0}^{N-1} \left\{a n+b-y(n)\right\} n \\ &=& 2 \sum_{n=0}^{N-1} a n^2+b n - y(n) n\ =\ 0 \end{eqnarray} と \begin{eqnarray} \frac{\partial}{\partial b}\varepsilon &=& \frac{\partial}{\partial b} \sum_{n=0}^{N-1} \left\{f(n)-y(n)\right\}^2 \\ &=& 2 \sum_{n=0}^{N-1} \left\{f(n)-y(n)\right\} \frac{\partial}{\partial b} f(n) \\ && 式(\ref{f0}) より \frac{\partial}{\partial b} f(n)=1\ だから \nonumber\\ &=& 2 \sum_{n=0}^{N-1} a n+b-y(n)\ =\ 0 \end{eqnarray} を連立させて解けばよく、行列で書くと次のようになります。 \begin{eqnarray} \left( \begin{array}{cc} \displaystyle\sum_{n=0}^{N-1} n^2 & \displaystyle\sum_{n=0}^{N-1} n \\ \displaystyle\sum_{n=0}^{N-1} n & \displaystyle\sum_{n=0}^{N-1} 1 \end{array} \right) \left( \begin{array}{c} a \\ \\ b \end{array} \right) &=& \left( \begin{array}{c} \displaystyle\sum_{n=0}^{N-1} y(n) n \\ \displaystyle\sum_{n=0}^{N-1} y(n) \end{array} \right) \end{eqnarray} つまり係数 \(a,b\) は \begin{eqnarray} \left( \begin{array}{c} a \\ \\ b \end{array} \right) &=& \left( \begin{array}{cc} \displaystyle\sum_{n=0}^{N-1} n^2 & \displaystyle\sum_{n=0}^{N-1} n \\ \displaystyle\sum_{n=0}^{N-1} n & \displaystyle\sum_{n=0}^{N-1} 1 \end{array} \right)^{-1} \left( \begin{array}{c} \displaystyle\sum_{n=0}^{N-1} y(n) n \\ \displaystyle\sum_{n=0}^{N-1} y(n) \end{array} \right) \end{eqnarray} ですが、総和公式 \begin{eqnarray} \displaystyle\sum_{n=0}^{N-1} n^2 &=& \displaystyle\frac{1}{6}(N-1)N(2N-1) \\ \displaystyle\sum_{n=0}^{N-1} n &=& \displaystyle\frac{1}{2}(N-1)N \\ \displaystyle\sum_{n=0}^{N-1} 1 &=& N \end{eqnarray} を代入して整理すると、\(2\times 2\) の逆行列の公式から \begin{eqnarray} \left( \begin{array}{c} a \\ \\ b \end{array} \right) &=& \frac{2}{N(N+1)} \left( \begin{array}{cc} \displaystyle\frac{6}{N-1} & -3 \\ -3 & 2N-1 \end{array} \right) \left( \begin{array}{c} \displaystyle\sum_{n=0}^{N-1} y(n) n \\ \displaystyle\sum_{n=0}^{N-1} y(n) \end{array} \right) \label{eq1} \end{eqnarray} のように簡単に求められます。特に \(N\) が固定の場合は、事前に \begin{eqnarray} \frac{2}{N(N+1)} \left( \begin{array}{cc} \displaystyle\frac{6}{N-1} & -3 \\ -3 & 2N-1 \end{array} \right) \label{eq2} \end{eqnarray} を展開して計算しておけばよいので、さらに高速に計算できます。

【注意】\(N\) が大きい場合、本アルゴリズムは使えません。式(\ref{eq1}),式(\ref{eq2}) 共に展開すると \(\frac{1}{N(N+1)(N-1)}\) となる係数があり、\(N\) が大きくなると行列の対角成分が急激に小さくなって計算誤差が大きくなるためです。 \(N\) が大きい場合は正規方程式を直接解かず、QR 分解や特異値分解などを使う方が安全です。

コード例

C++ のコーディング例を以下に示します。


	const int N = 1000;

	const double t1 = 12.0        /(N*(N*N-1));
	const double t2 = -6.0        /(N*(N+1));
	const double t3 =  2.0*(2*N-1)/(N*(N+1));

	double y[N];
	//   :
	// ここで y[n] にデータを入力する
	//   :

	double sum1=0,sum2=0;
	for (int n=0; n<N; n++)
	{
		sum1+=y[n]*n;
		sum2+=y[n];
	}

	double a = t1*sum1+t2*sum2;
	double b = t2*sum1+t3*sum2;

	cout << "a=" << a << ", b=" << b << endl;

実験

本方式によりノイズ混じりデータに直線を当てはめた例を以下に示します。

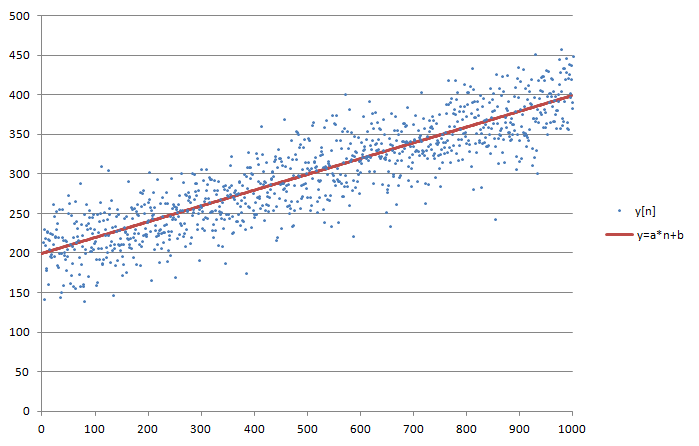
右上がりの傾向を表す直線が正しく得られています。