チェビシェフの不等式
概要
チェビシェフの不等式は、期待値から外れた現象がどのくらいの確率で生じるかを見積もることができる便利な公式で、 どのような確率分布を持つ場合にも成り立ちます。
\(X\) を確率変数、その期待値を \( \mu \)、分散を \( \sigma^2 \) とすると、チェビシェフの不等式は次のように表せます。 \begin{eqnarray} Pr(|X-\mu|\geq k)\leq\frac{\sigma^2}{k^2} \end{eqnarray}
証明
どのような確率分布でもチェビシェフの不等式が成り立つことを証明します。
\(X\) の分散 \(\sigma^2\) は次のように表せる。
\begin{eqnarray}
\sigma^2
&=& \int_{-\infty}^{+\infty} (X-\mu)^2 f(X) dX \\
&& 積分区間を 3 つに分割して \nonumber\\
&=& \underbrace{\int_{-\infty}^{\mu-k} (X-\mu)^2 f(X) dX}_{A} + \underbrace{\int_{\mu-k}^{\mu+k} (X-\mu)^2 f(X) dX}_{B} + \underbrace{\int_{\mu+k}^{+\infty} (X-\mu)^2 f(X) dX}_{C} \label{sigma}
\end{eqnarray}
確率密度関数 \(f(X)\) は非負だから \(A,B,C\) いずれも非負である。
非負の項を取り除けば、右辺は減少するか変化しないかどちらかだから、\(B\) を取り除いた場合、次の関係が成り立つ。
\begin{eqnarray}
\sigma^2
&\geq& \underbrace{\int_{-\infty}^{\mu-k} (X-\mu)^2 f(X) dX}_{A} + \underbrace{\int_{\mu+k}^{+\infty} (X-\mu)^2 f(X) dX}_{C}
\end{eqnarray}
\(A\) の区間は \(X\leq\mu-k\)、\(C\) の区間は \(\mu+k\leq X\) だから、まとめて
\begin{eqnarray}
|X-\mu|\geq k
\end{eqnarray}
と書ける。両辺を 2 乗すれば
\begin{eqnarray}
|X-\mu|^2 = (X-\mu)^2 \geq k^2 \label{Xmu}
\end{eqnarray}
だから
\begin{eqnarray}
\sigma^2
&\geq& \int_{-\infty}^{\mu-k} (X-\mu)^2 f(X) dX + \int_{\mu+k}^{+\infty} (X-\mu)^2 f(X) dX \\
&& 式(\ref{Xmu})から (X-\mu)^2\geq k^2 であり、確率密度関数 f(x) は非負だから \nonumber\\
&\geq& \int_{-\infty}^{\mu-k} k^2 f(X) dX + \int_{\mu+k}^{+\infty} k^2 f(X) dX \\
&& 積分区間をひとまとめに書けば \nonumber\\
&=& k^2 \int_{|X-\mu|\geq k} f(X) dX \\
&& k^2 以外の部分は |X-\mu|\geq k となる確率を表しているので \nonumber\\
&=& k^2 Pr(|X-\mu|\geq k)
\end{eqnarray}
両辺を \(k^2\) で割れば
\begin{eqnarray}
Pr(|X-\mu|\geq k) &\leq& \frac{\sigma^2}{k^2} \label{ChebyshevIneq}
\end{eqnarray}
証明の過程で確率分布には何の制限も加えなかったので、どのような確率分布でも式(\ref{ChebyshevIneq})は成り立つ。
実験
\(0\leq X\leq 1\) の値を等確率で生じる一様分布を例に、チェビシェフの不等式が成り立つか試してみましょう。
\(X\) の値域が \(0\leq X\leq 1\) に限られることと、全確率が 1 であることから、この場合の確率密度関数 \( f(X) \) は \begin{eqnarray} f(X) = \left\{ \begin{array}{cc} 1,& 0 \leq X \leq 1 \\ 0,& その他 \end{array} \right.\label{fX} \end{eqnarray} で表わせ、期待値 \( \mu \) と分散 \( \sigma^2 \) は、次のようになります。 \begin{eqnarray} \mu &=& \int_{-\infty}^{+\infty} X f(X) dX \\ && 式(\ref{fX}) より \\ &=& \int_0^1 X dX = \left[\frac{1}{2}X^2\right]_0^1 \\ &=& \frac{1}{2} \label{UniformMu}\\ \sigma^2 &=& \int_{-\infty}^{+\infty} (X-\mu)^2 f(X) dX \\ && 式(\ref{fX}) より \\ &=& \int_0^1 (X-\mu)^2 dX = \int_0^1 X^2-2\mu X+\mu^2\ dX \\ && 式(\ref{UniformMu})より \mu=\frac{1}{2} だから \nonumber\\ &=& \int_0^1 X^2-X+\frac{1}{4}\ dX = \left[ \frac{1}{3}X^3-\frac{1}{2}X^2+\frac{1}{4}X \right]_0^1 = \frac{1}{3}-\frac{1}{2}+\frac{1}{4} \\ &=& \frac{1}{12} \label{UniformSigma2} \end{eqnarray} この場合、期待値 \(\mu=\displaystyle\frac{1}{2}\) から \(k\) 以上離れた \(X\) が生じる確率は、下図の赤い部分の面積ですから \begin{eqnarray} Pr\left(\left|X-\frac{1}{2}\right|\geq k\right) = 1-2k \label{prXmu} \end{eqnarray} になります (\(X\) が 0 未満や 1 を超える値になることはありませんので \(0\leq k\leq \displaystyle\frac{1}{2}\) の範囲で考えます)。
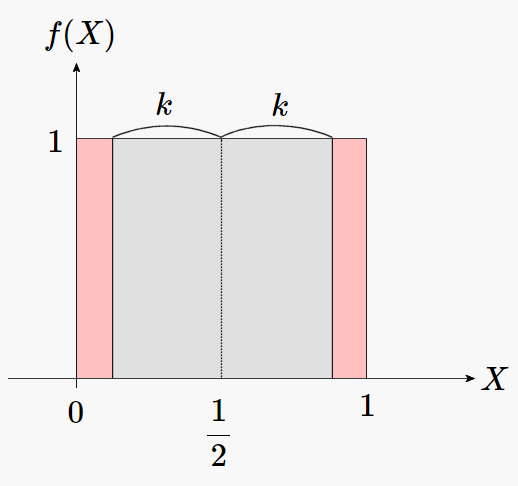
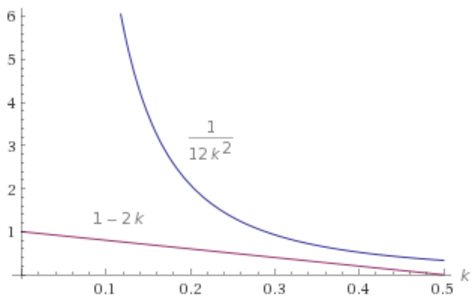
確かに \(1-2k\) は \(\displaystyle\frac{1}{12 k^2}\) の下にあり、 \(0\leq k\leq \displaystyle\frac{1}{2}\) の範囲でチェビシェフの不等式が成り立っています。