矩形波で円周率 \(\pi\) を求める
\begin{eqnarray} \pi &=& 4 \left( 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \right) \nonumber \end{eqnarray} を導きます。
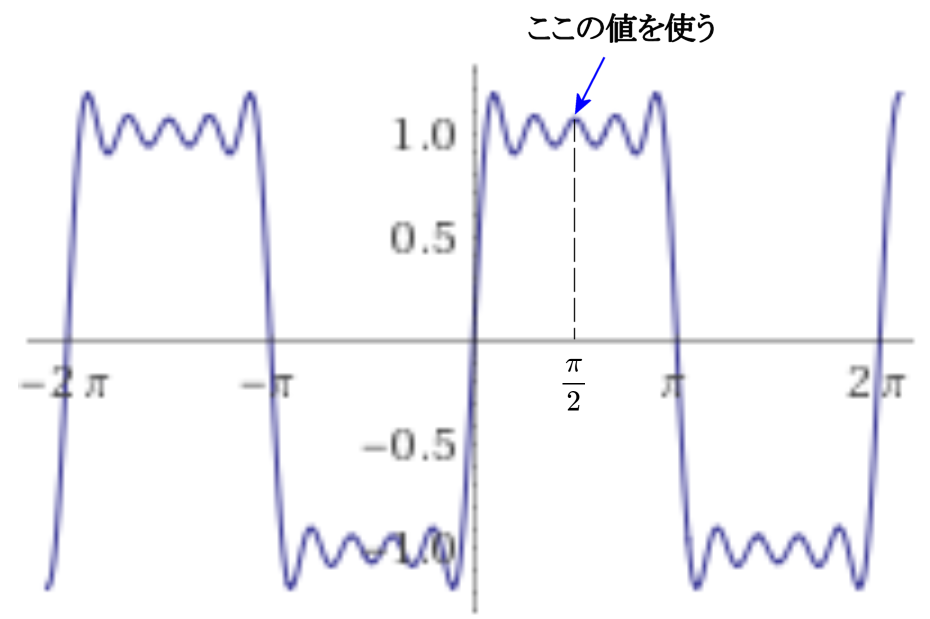
矩形波のフーリエ級数展開(図は最初の5項までの部分和)
矩形波のフーリエ級数
周期 \(2\pi\) の矩形波を \(f(x)\) と書き、\(\pm\pi\) の範囲で次のように表すことにします。 \begin{eqnarray} f(x) &=& \left\{ \begin{array}{cc} -1, & -\pi\leq x\lt 0 \\ +1, & 0\leq x\lt \pi \end{array} \right. \label{fx} \end{eqnarray} 奇関数ですから\(f(x)\)をフーリエ級数展開すると \begin{eqnarray} f(x) &\sim& \sum_{n=1}^\infty b_n\sin(n x) \end{eqnarray} と表わせ、フーリエ係数 \(b_n\) は次のように計算できます。 \begin{eqnarray} b_n &=& \frac{1}{\pi}\int_{-\pi}^{+\pi} f(x) \sin(nx) dx \\ & & f(x) と \sin(nx) は共に奇関数で、その積は偶関数になるから \nonumber\\ &=& \frac{2}{\pi} \int_0^\pi \sin(nx) dx \\ & & \int \sin(nx) dx = -\frac{1}{n}\cos (n x) より \nonumber\\ &=& -\frac{2}{n\pi} \left[\cos(nx)\right]_{0}^{\pi} \\ &=& -\frac{2}{n\pi} \left\{\cos(n\pi)-1\right\} \\ &=& \frac{2}{n\pi} (1-\cos(n\pi)) \\ &=& \left\{ \begin{array}{cc} \displaystyle\frac{4}{n\pi},& n=1,3,5,7,\cdots\\ 0,& n=2,4,6,8,\cdots \end{array} \right. \end{eqnarray} \(n\) が偶数の項は \(b_n=0\) で、\(n\) が奇数の項だけが残りますので、\(n=2k-1\) として、次のように書けます。 \begin{eqnarray} f(x) &\sim& \sum_{k=1}^\infty \displaystyle\frac{4}{(2k-1)\pi}\sin\{(2k-1)x\} \\ &=& \frac{4}{\pi} \left\{ \sin(x) + \frac{1}{3}\sin(3x) + \frac{1}{5}\sin(5x) + \frac{1}{7}\sin(7x)+ \cdots \right\} \label{rectangle} \end{eqnarray}
グレゴリー・ライプニッツの公式
\(f(x)\) が連続な所では式(\ref{rectangle})が成り立ちますので、\(f(x)\) が連続な区間にある \(x=\displaystyle\frac{\pi}{2}\) を代入して \begin{eqnarray} 1 &=& \frac{4}{\pi} \left\{ \sin\left(\frac{\pi}{2}\right) + \frac{1}{3}\sin\left(\frac{3\pi}{2}\right) + \frac{1}{5}\sin\left(\frac{5\pi}{2}\right) + \frac{1}{7}\sin\left(\frac{7\pi}{2}\right) + \cdots \right\} \\ &=& \frac{4}{\pi} \left( 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \right) \end{eqnarray} 両辺に \(\pi\) を掛ければ \begin{eqnarray} \pi &=& 4 \left( 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \right) \label{pi} \end{eqnarray} が得られます。この式はグレゴリー・ライプニッツの公式として知られています。
天は二物を与えず
下表はグレゴリー・ライプニッツの公式の第 \(N\) 項までの部分和 \(p_N\)
\begin{eqnarray}
p_N &=& 4 \left\{ 1 - \frac{1}{3} + \frac{1}{5} - \frac{1}{7} + \cdots \frac{(-1)^{N+1}}{2N-1}\right\}
\end{eqnarray}
を計算したものです (正しい円周率は 3.14159265358979… であり、表の赤字部分は正しくありません)。
| 項数 \(N\) | 部分和 \(p_N\) | 正しい桁数 |
|---|---|---|
| 1 | 4.000000000 | なし |
| 10 | 3.041839619 | 1桁 |
| 100 | 3.131592904 | 2桁 |
| 1,000 | 3.140592654 | 3桁 |
| 10,000 | 3.141492654 | 4桁 |
| 100,000 | 3.141582654 | 5桁 |
| 1,000,000 | 3.141591654 | 6桁 |
百万項計算しても 6 桁しか合っていないのでは、悲しくなってしまいます。グレゴリー・ライプニッツの公式はシンプルで大変美しいのですが、円周率の計算には向いていません。数式も「天は二物を与えず」ですね。
関連項目