ギブスの現象をやさしく丁寧に解説
概要
ギブスの現象は不連続な関数をフーリエ級数展開すると、不連続点の近くで元の関数に収束せず、角が飛び出たようになる現象です。
人名 Gibbs をどう読むかで「ギブズの現象」や「ギップスの現象」と書かれていることもあります。
矩形波のフーリエ級数展開
周期 \(2\pi\) の
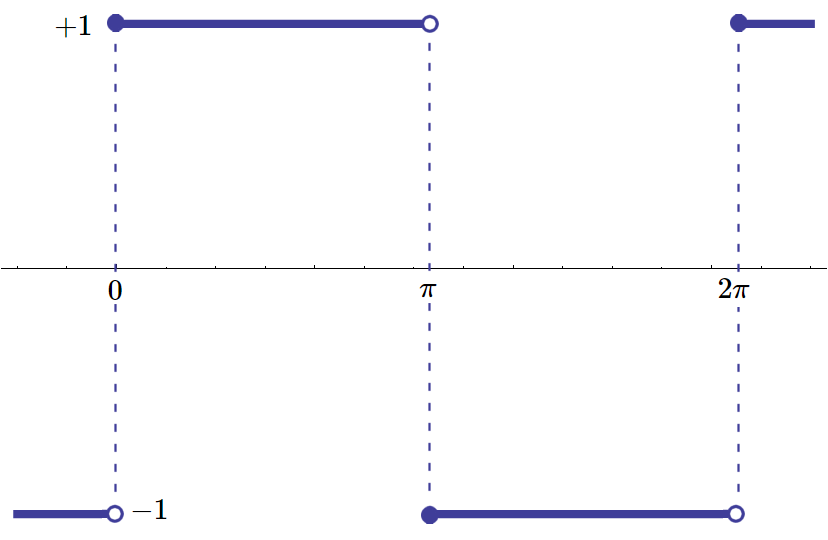
矩形波 \(f(t)\)
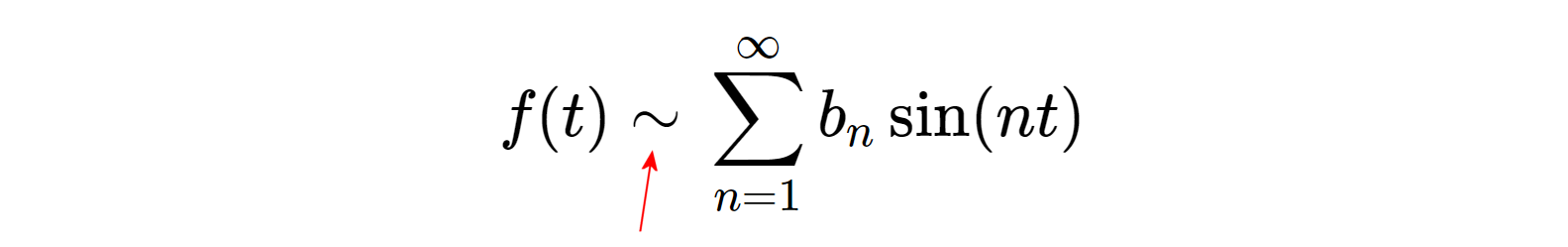
何だ、この自信なさそうなニョロニョロは?!
計算してみると…
実際に式 (\ref{fhat(t)}) の右辺を計算してみましょう。係数 \(b_n\) は \begin{eqnarray} b_n &=& \frac{1}{\pi}\int_{0}^{2\pi} f(t) \sin(n t)dt \\ &=& \frac{1}{\pi}\left\{\int_{0}^{\pi} \sin(n t)dt - \int_{\pi}^{2\pi} \sin(n t)dt \right\} \\ &=& \frac{1}{\pi}\left\{ \left[-\frac{1}{n}\cos(n t)\right]_{0}^{\pi} - \left[-\frac{1}{n}\cos(n t)\right]_{\pi}^{2\pi} \right\} \\ &=& \frac{-1}{n\pi}\left\{ \left(\cos n\pi - \cos 0\right) - \left(\cos(2n\pi)-\cos(n\pi)\right) \right\} \\ &=& \frac{-1}{n\pi}\left\{ \cos n\pi - \cos 0 - \cos(2n\pi) + \cos(n\pi) \right\} \\ &=& \frac{-2}{n\pi}\left\{ \cos(n\pi) - 1 \right\} \\ &=& \frac{2}{n\pi}\left\{ 1 - \cos(n\pi) \right\} \\ & & \cos(n\pi) = \left\{ \begin{array}{ll} -1, & n=1,3,5,7,\cdots \\ +1, & n=2,4,6,8,\cdots \\ \end{array} \right. \mbox{より} \nonumber\\ &=& \left\{ \begin{array}{ll} \displaystyle\frac{4}{n\pi}, & n=1,3,5,7,\cdots \\[1em] 0, & n=2,4,6,8,\cdots \\ \end{array} \right. \end{eqnarray} と、偶数次の係数が全部 0 になりますので、奇数 \(n=2m-1\) 次の項だけを使って式 (\ref{fhat(t)}) の右辺を \begin{eqnarray} g(t) &=& \sum_{m=1}^\infty \frac{4}{(2m-1)\pi} \sin\{(2m-1)t\} \\ &=& \lim_{M\to\infty} \frac{4}{\pi} \sum_{m=1}^M \frac{1}{2m-1} \sin\{(2m-1)t\} \label{ftlim} \end{eqnarray} と書くことにし、総和を \(M\) までで打ち切った部分和を \begin{eqnarray} g_M(t) &=& \frac{4}{\pi} \sum_{m=1}^M \frac{1}{2m-1} \sin\{(2m-1)t\} \label{tM} \end{eqnarray} で表すことにすると、\(g_1(t),\ g_4(t),\ g_{16}(t),\ g_{64}(t),\ g_{256}(t)\) は次のようなグラフになります。
| \(g_1(t)\) | 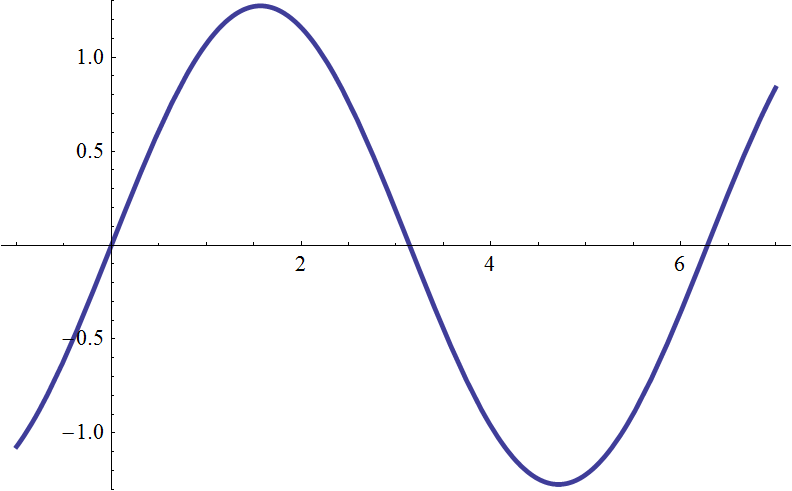 |
|---|---|
| 正弦波 1 本だけで矩形波を近似 | |
| \(g_4(t)\) | 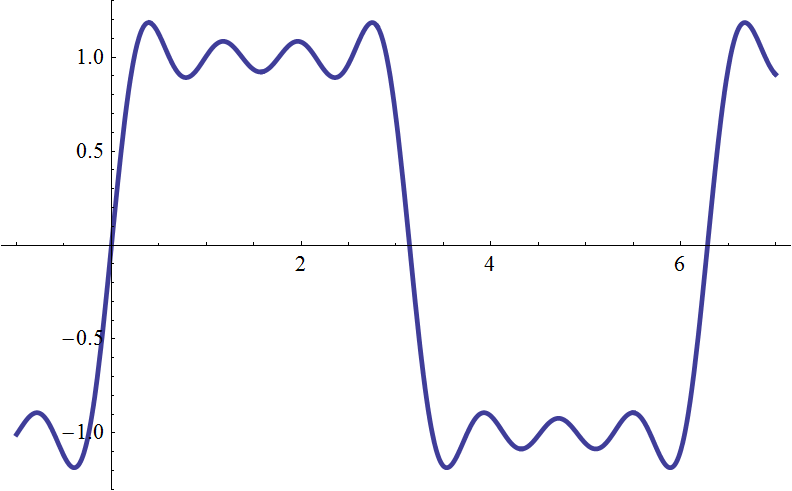 |
| 正弦波 4 本でも、それなりに四角くなる | |
| \(g_{16}(t)\) | 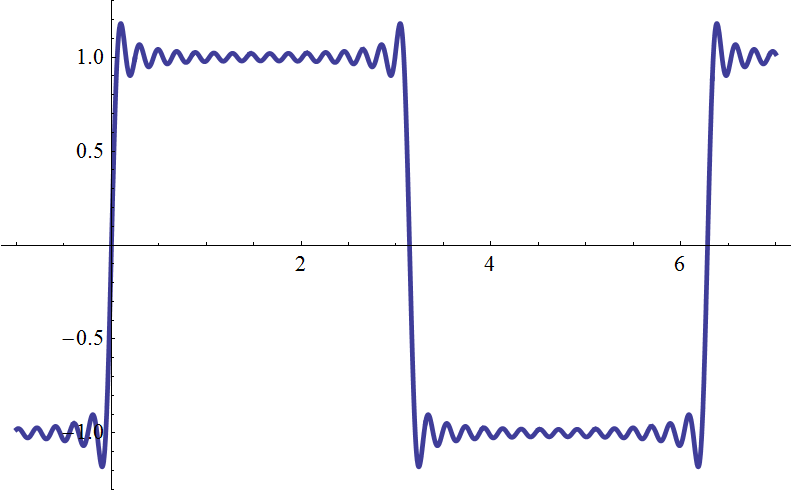 |
| 16 本使うと、かなり四角くなるが、不連続点付近の振動が気になる | |
| \(g_{64}(t)\) | 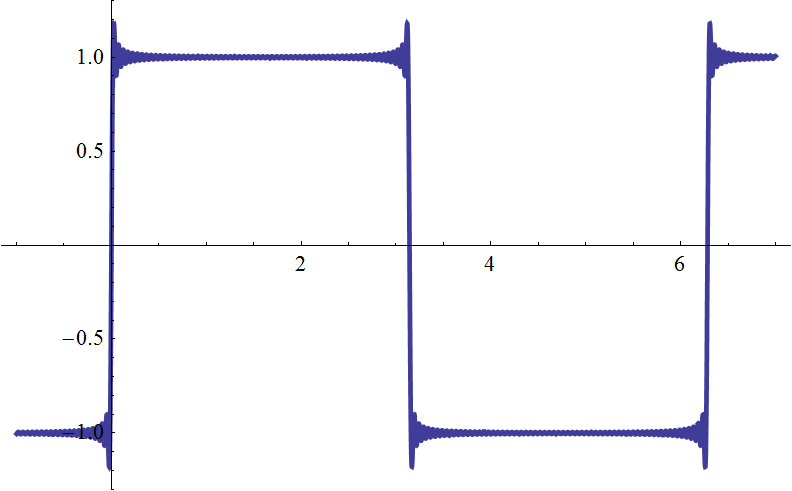 |
| 64 本では振動は細かくなるが、突き出た部分の大きさは変化なし? | |
| \(g_{256}(t)\) | 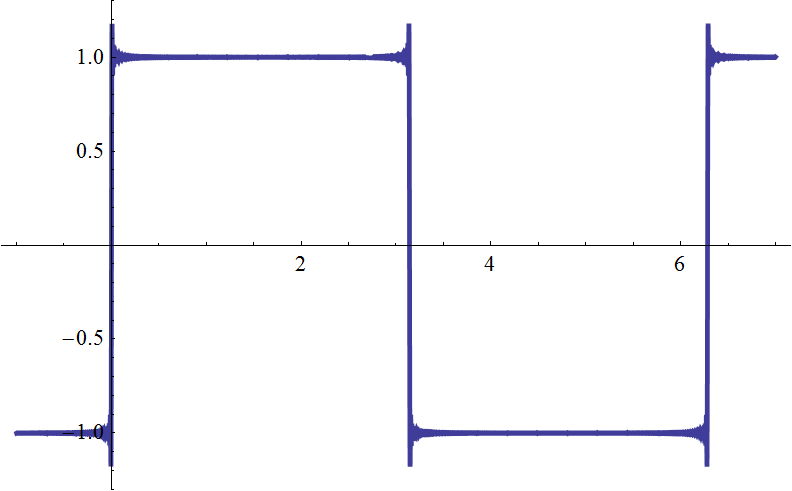 |
| いくらやっても突き出た部分が小さくならないぞ! |
正弦波を沢山足し合わせるほど、振動は \(f(t)\) の不連続点 (\(\pi\) の整数倍) 付近に集中してゆくようですが、 上下にツンと突き出た細い針のような「角」は、飛び出たまま小さくならないようです。
上に突き出た部分を拡大して重ね描きしてみましょう (区別しやすくするため、色分けしています)。
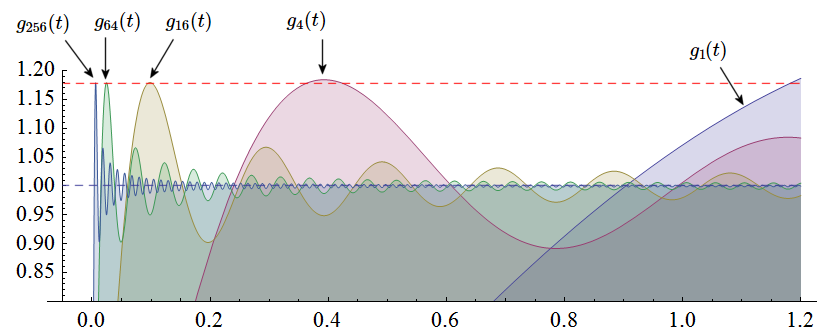 |
| \(g_1(t), g_4(t), g_{16}(t), g_{64}(t), g_{256}(t)\) のグラフ上部を拡大して重ね描き |
\(M\) を \(1,4,16,64,256\) と大きくするほど「角」は左に寄り、そのピーク値は \(1.18\) 辺りに近づいてゆくように見えます (本当は 1 に収束してほしいです) が、 収束の遅い級数はいくらでもありますので、この実験だけで \(g_M(t)\) のピーク値が \(M\to\infty\) で \(1.18\) 付近に収束するとはいえません。
調べてみましょう。
「角」のピーク値
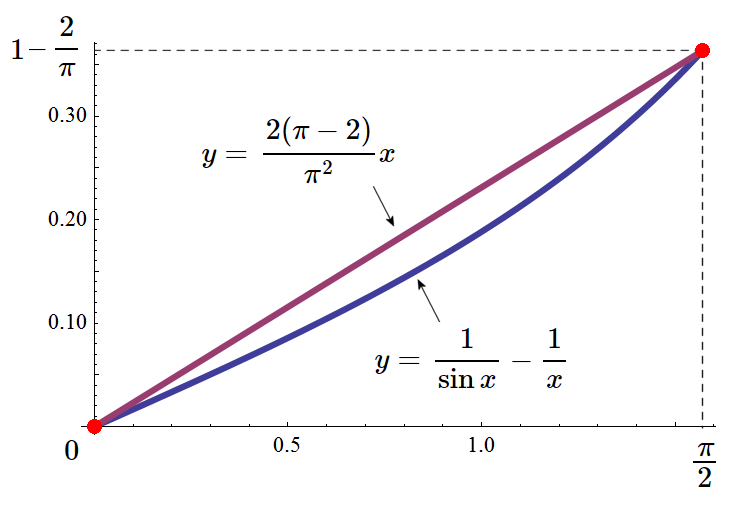
フーリエ級数 \(g(t)\) の \(M\) 項までの部分和 \begin{eqnarray} g_M(t) &=& \frac{4}{\pi} \sum_{m=1}^M \frac{1}{2m-1} \sin\{(2m-1)t\} \nonumber \end{eqnarray} の \(t=0\) 付近にある最大の「角」の位置を \(t_p\) と書くことにすると、「角」の頂点では \(g'_M(t_p)=0\) になるはずですから、 \begin{eqnarray} g'_M(t) &=& \frac{4}{\pi} \frac{d}{dt} \sum_{m=1}^M \frac{1}{2m-1} \sin\{(2m-1)t\} \\ &=& \frac{4}{\pi} \sum_{m=1}^M \frac{1}{2m-1} \frac{d}{dt} \sin\{(2m-1)t\} \\ &=& \frac{4}{\pi} \sum_{m=1}^M \cos\{(2m-1)t\} \\ &=& \frac{4}{\pi} \sum_{m=1}^M Re\left[e^{i(2m-1)t}\right] \\ &=& \frac{4}{\pi} Re\left[ \sum_{m=1}^M e^{i(2m-1)t} \right] \\ & & \sum_{m=1}^M e^{i(2m-1)t} は初項 e^{it} 公比 e^{2it} の等比数列の和ですから \nonumber\\ &=& \frac{4}{\pi} Re\left[ e^{it} \frac{1-e^{2i M t}}{1-e^{2it}} \right] \\ &=& \frac{4}{\pi} Re\left[ e^{it} \frac{1-e^{2i M t}}{1-e^{2it}} \cdot \frac{1-e^{-2it}}{1-e^{-2it}} \right] \\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})e^{it}(1-e^{-2it})}{1-e^{2it}-e^{-2it}+1}\right] \\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})(e^{it}-e^{-it})}{2-e^{2it}-e^{-2it}}\right] \\ & & e^{it}-e^{-it}=2i\sin t\ かつ\ e^{2it}+e^{-2it} = 2\cos(2t) なので \nonumber\\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})2i\sin t}{2-2\cos(2t)}\right] \\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})i\sin t}{1-\cos(2t)}\right] \\ & & 1-\cos(2t) = 2\sin^2 t ですから \nonumber\\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})i\sin t}{2\sin^2 t}\right] \\ &=& \frac{4}{\pi} Re\left[ \frac{(1-e^{2i M t})i}{2\sin t}\right] \\ &=& \frac{4}{\pi} \frac{1}{2\sin t} Re[ i-i\left\{\cos(2M t)+i\sin(2M t)\right\}] \\ &=& \frac{4}{\pi} \frac{1}{2\sin t} Re[ i-i\cos(2M t)+\sin(2M t)] \\ &=& \frac{4}{\pi} \frac{\sin(2M t)}{2\sin t} \\ &=& \frac{2}{\pi} \frac{\sin(2M t)}{\sin t} \label{sin2Mt}\\ &=& 0 \end{eqnarray} を解いて、\(t=0\) に一番近くて一番大きい「角」の頂点は、式(\ref{sin2Mt})の分子が \(\sin(2M t)=0\) になる \begin{eqnarray} t_p &=& \frac{\pi}{2M} \end{eqnarray} にあることがわかります。 一般に \begin{eqnarray} f(t) &=& \int_0^t f'(x) dx - f(0) \end{eqnarray} が成り立ちますので、\(g_M(0)=0\) であることから \(g_M(t)\) は \begin{eqnarray} g_M(t) &=& \int_0^t g'_M(x) dx - g_M(0) \\ && g'_M(x) に式(\ref{sin2Mt}) を代入して \nonumber\\ &=& \frac{2}{\pi} \int_0^t \frac{\sin(2M x)}{\sin x} dx \end{eqnarray} と書けます。ここでちょっと細工をして次のようにしましょう。 \begin{eqnarray} g_M(t) &=& \frac{2}{\pi} \int_0^t \frac{\sin(2M x)}{\sin x} dx \nonumber\\ &=& \frac{2}{\pi} \int_0^t \left(\frac{1}{\sin x}+\underbrace{\frac{1}{x}-\frac{1}{x}}_{ここがミソ}\right)\sin(2M x) dx \\ &=& \frac{2}{\pi} \underbrace{\int_0^t \left(\frac{1}{\sin x}-\frac{1}{x}\right)\sin(2M x) dx}_{I_1(t)} + \frac{2}{\pi} \underbrace{\int_0^t \frac{\sin(2M x)}{x}dx}_{I_2(t)} \label{1sinx1x} \end{eqnarray} すると \(y=\displaystyle\frac{1}{\sin x}-\frac{1}{x}\) のグラフは下図のように \((0,0)\) と \((\displaystyle\frac{\pi}{2},1-\frac{2}{\pi})\) を通り、 この範囲では両端を結ぶ直線 \(y=\displaystyle\frac{2(\pi-2)}{\pi^2}x\) より大きくなることがない「 下に凸な関数 」ですので、次の不等式が成り立ちます。 \begin{eqnarray} 0\leq \frac{1}{\sin x}-\frac{1}{x} \leq \frac{2(\pi-2)}{\pi^2}x \end{eqnarray}
ここに現れた \(Si(x)=\displaystyle\int_0^x \frac{\sin(y)}{y} dy\) は「正弦積分」という特殊関数で、 \(x=\pi\) での値は \(1.85193705\cdots\) ですので、\(\displaystyle\frac{2}{\pi}\) を掛けた収束先は、残念ながら \(1\) ではなく \(1.17897974\cdots\) になってしまいます。 \begin{eqnarray} \frac{2}{\pi}Si(\pi) &\simeq& 1.17897974 \quad \cdots ギブスの定数 \end{eqnarray}
さきほどの図 (下に再掲) でピークの収束先が \(1.18\) 付近に見えたのは、この値だったのです。
 |
| \(g_1(t), g_4(t), g_{16}(t), g_{64}(t), g_{256}(t)\) のグラフ上部を拡大して重ね描き |
不連続な関数をフーリエ級数展開すると、このように不連続点の近くで元の関数値に収束せず、「角」が飛び出てしまう現象を「ギブスの現象」といいます。
フーリエ級数を有限な \(M\) で打ち切った時に「角」が出るのは少しも不思議ではありませんが、 不連続点があると \(M\) をいくら大きくしても「角」が消えずに残ってしまうところが、この現象の真に驚くべき点です。
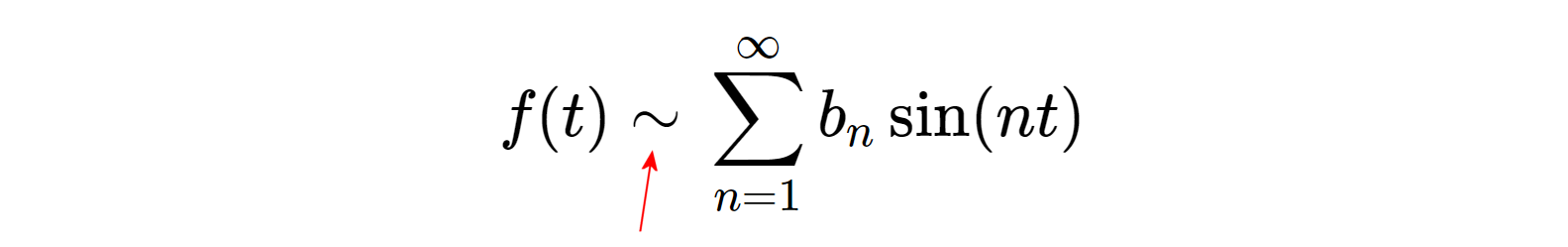
だから '\(=\)' とは書けなかったのね…
トリビア
この現象、「ギブスの現象」と呼ばれていますが、最初に発見したのはギブスさん (Josiah Willard Gibbs, 1839~1903年) ではなく、光速の測定で有名なアルバート・マイケルソンさん (Albert Abraham Michelson, 1852~1931年)です。
マイケルソンさんが作る実験装置の精度は折り紙つきで、誰もが認める「実験の天才」だったのですが、 フーリエ級数の合成装置を作り、数式どおりにノコギリ波を合成してみたところ、出力された波形には変な「角」ができてしまいました。
「正弦波の本数が足りないのかもしれない」と思って 80 項まで合成しても「角」は消えず、まじめなマイケルソンさんは「こんな目で見えるほど大きな誤差が出るのは、自分の設計が悪いんだ」と、人知れず悩み続けたようです。 当時、フーリエ級数にそんな「角」があるなんて、誰も知らなかったのですから無理もありません。
考えに考え、改良に改良を重ねても、合成装置から出力される波形の「角」は消えませんでした。機械に頼らず手で計算してみても、やはり「角」が現れます。
とうとう万策尽きて「何故かうまくいかない」とこぼしたところ、それを聞いた数学者のギブスさんが、あれこれ考えて原因を解明してくれたのだそうで…。まるで映画みたいなストーリーですね。
19世紀末に 80 オシレーターの正弦波合成シンセを作ったマイケルソンさんも凄いですが、「そんなの誤差だろ」で済ませず原因を突き止めたギブスさんも凄い!