単位分数の和

単位分数の和の問題を解いてみました。

問題

自然数 $a,b,c$ で \begin{eqnarray} \displaystyle\frac{1}{a}+\frac{1}{b}+\frac{1}{c}=1 \label{Q} \end{eqnarray} かつ \begin{eqnarray} a\leq b\leq c \label{order} \end{eqnarray} を満たすものを全て求めよ。

解答

式(\ref{order})の逆数を取ると \begin{eqnarray} \frac{1}{c}\leq \frac{1}{b}\leq \frac{1}{a} \end{eqnarray}

$a$ の範囲

$\displaystyle\frac{1}{a}$ は $\displaystyle\frac{1}{c}$ よりも $\displaystyle\frac{1}{b}$ よりも大きいのだから、以下が成り立つ。 \begin{eqnarray} \displaystyle \frac{1}{a}+\frac{1}{b}+\frac{1}{c} \leq \frac{1}{a}+\frac{1}{a}+\frac{1}{a} \end{eqnarray} 式(\ref{Q})より、左辺 = 1 だから \begin{eqnarray} \displaystyle 1 \leq \frac{3}{a} \end{eqnarray} $a$ は自然数 ($1\leq a$) なので、両辺を$a$ 倍しても不等号の向きは変わらない。 \begin{eqnarray} a \leq 3 \end{eqnarray} よって $a$ は 1,2,3 のどれかである。

$c$ を $a,b$ で表す

さて、式(\ref{Q})の両辺を $abc$ 倍して項を並べ替えると \begin{eqnarray} ab+bc+ca=abc \end{eqnarray} ここで $c$ に注目して、次のように書き換えてゆく。 \begin{eqnarray} ab+(a+b)c &=& abc \\ ab &=& abc-(a+b)c \\ ab &=& (ab-a-b)c \\ \end{eqnarray} よって \begin{eqnarray} c &=& \frac{ab}{ab-a-b} \end{eqnarray} これを $a$ に依存する $b$ の関数と考え \begin{eqnarray} c_a(b) &=& \frac{ab}{ab-a-b} \end{eqnarray} と書くことにする。

$a=1$ の場合

式(\ref{Q})に $a=1$ を代入すると \begin{eqnarray} \require{cancel} \cancel{1}+\frac{1}{b}+\frac{1}{c}=\cancel{1} \end{eqnarray} \begin{eqnarray} \frac{1}{c}=-\frac{1}{b} \end{eqnarray} となり、$c$ は自然数で負になり得ないから $a=1$ は不適である。

$a=2$ の場合

$a=2$ の場合、$c_2(b)$ は次のようになる。 \begin{eqnarray} c_2(b) &=& \frac{2b}{2b-2-b} &=& \frac{2b}{b-2} \end{eqnarray}

$c_2(b)$ の微分は \begin{eqnarray} c_2'(b) &=& \frac{2(b-2)-2b}{(b-2)^2}&=& \frac{\cancel{2b}-4-\cancel{2b}}{(b-2)^2} &=& -\left(\frac{2}{b-2}\right)^2 \lt 0 \end{eqnarray} と常に負 ($b$ に対して単調減少) で、$b$ が増加すると $c$ は減少するため、どこかで $c=b$ になる。それは \begin{eqnarray} c_2(b) &=& \frac{2b}{b-2} &=& b \end{eqnarray} になる時、つまり \begin{eqnarray} 2b &=& b(b-2) &=& b^2-2b \end{eqnarray} より \begin{eqnarray} b^2-4b &=& b(b-4) &=& 0 \end{eqnarray} が成り立つ時だが、$b$ は自然数なので $b=0$ は除外し、$b=4$ が上限ということになる。

$a\leq b$ でなければならないが、$a=b=2$ では $c_2(2)=\infty$ になってしまうので、$3\leq b$ でなければならず、$a=2$ の場合に可能な $b$ は 3 と 4 に限られる。

それぞれに対応する $c_2(b)$ を計算すると \begin{eqnarray} c_2(3) &=& \frac{2\cdot 3}{3-2} &=& 6 \\ c_2(4) &=& \frac{2\cdot 4}{4-2} &=& 4 \end{eqnarray} よって $a=2$ の場合に可能な組み合わせは $(a,b,c)=(2,3,6),(2,4,4)$ の 2 つしかない。

$a=3$ の場合

$a=3$ の場合、$c_3(b)$ は次のようになる。 \begin{eqnarray} c_3(b) &=& \frac{3b}{3b-3-b} &=& \frac{3b}{2b-3} \end{eqnarray} $b$ が自然数で $b=\displaystyle\frac{3}{2}$ ではあり得ず、$c_3(b)$ の微分は \begin{eqnarray} c_3'(b) &=& \frac{3(2b-3)-3b\cdot 2}{(2b-3)^2}&=& \frac{\cancel{6b}-9-\cancel{6b}}{(2b-3)^2} &=& -\left(\frac{3}{2b-3}\right)^2 \lt 0 \end{eqnarray} と常に負 ($b$ に対して単調減少) で、$b$ が増加すると $c$ は減少するため、どこかで $c=b$ になる。それは \begin{eqnarray} c_3(b) &=& \frac{3b}{2b-3} &=& b \end{eqnarray} になる時、つまり \begin{eqnarray} 3b &=& b(2b-3) &=& 2b^2-3b \end{eqnarray} より \begin{eqnarray} 2b^2-6b &=& 2b(b-3) &=& 0 \end{eqnarray} が成り立つ時だが、$b$ は自然数なので $b=0$ を除外し、$b=3$ が上限ということになる。

従って $a\leq b$ であることを考えると、$a=3$ の場合は $b=3$ しかあり得ない。

対応する $c$ を計算すると \begin{eqnarray} c_3(3) &=& \frac{3\cdot 3}{2\cdot 3-3} &=& \frac{9}{3} &=& 3 \end{eqnarray} つまり $a=3$ の場合に可能な組み合わせは $(a,b,c)=(3,3,3)$ しかない。

結論

式(\ref{Q}),式(\ref{order}) を満たす自然数 $a,b,c$ は \begin{eqnarray} (a,b,c)=(2,3,6),(2,4,4),(3,3,3) \end{eqnarray} の 3 組だけである。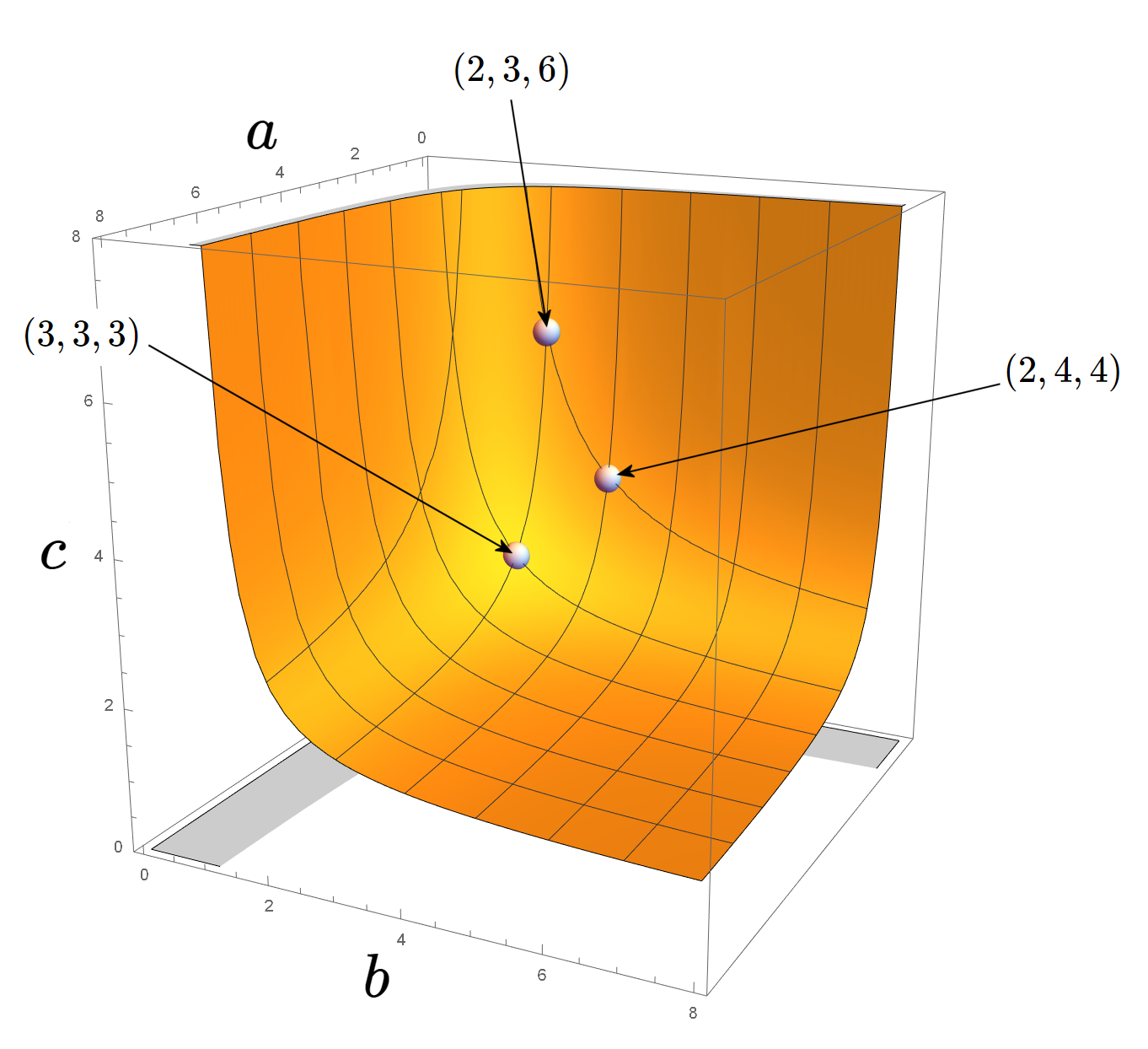

図1 : 曲面 $c_a(b)=\displaystyle\frac{ab}{ab-a-b}$ 上の自然数点 $(a,b,c)$ は 3 つしかない