多項式当てはめにリッジ回帰を併用する際の注意点
多項式回帰
データ \((x_0, y_0), (x_1, y_1), (x_2, y_2), \cdots (x_{N-1}, y_{N-1})\) に多項式 \begin{eqnarray} f(x,\boldsymbol{a}) &=& \sum_{m=0}^M a_m x^m,\quad \boldsymbol{a}=(a_0,a_1,a_2,\cdots a_M)^T \end{eqnarray} を最小二乗法で当てはめることを考えます。
誤差評価関数を \begin{eqnarray} J(\boldsymbol{a}) = \sum_{n=0}^{N-1}\left\{ f(x_n,\boldsymbol{a}) - y_n \right\}^2 \end{eqnarray} として \begin{eqnarray} \frac{\partial J(\boldsymbol{a})}{\partial \boldsymbol{a}} &=& \boldsymbol{0} \end{eqnarray} を計算すると、以下の正規方程式が得られます。 \begin{eqnarray} \boldsymbol{X}\boldsymbol{a} &=& \boldsymbol{Y} \label{sq}\\ && \boldsymbol{X} = \left( \begin{array}{cccc} \displaystyle\sum_{n=0}^{N-1} x_n^0 & \displaystyle\sum_{n=0}^{N-1} x_n^1 & \cdots & \displaystyle\sum_{n=0}^{N-1} x_n^M \\ \displaystyle\sum_{n=0}^{N-1} x_n^1 & \displaystyle\sum_{n=0}^{N-1} x_n^2 & \cdots & \displaystyle\sum_{n=0}^{N-1} x_n^{M+1} \\ \vdots & & \ddots & \vdots\\ \displaystyle\sum_{n=0}^{N-1} x_n^M & \displaystyle\sum_{n=0}^{N-1} x_n^{M+1} & \cdots & \displaystyle\sum_{n=0}^{N-1} x_n^{2M} \\ \end{array} \right) \\ && \boldsymbol{Y} = \left( \begin{array}{cccc} \displaystyle\sum_{n=0}^{N-1} y_n x_n^0 \\ \displaystyle\sum_{n=0}^{N-1} y_n x_n^1 \\ \vdots \\ \displaystyle\sum_{n=0}^{N-1} y_n x_n^M \\ \end{array} \right) \end{eqnarray} 式(\ref{sq})を解けば、多項式係数 \(\boldsymbol{a}=(a_0,a_1,a_2,\cdots a_M)^T\) が求まります。
リッジ回帰
リッジ回帰 (ridge regression) では多項式係数が大きくなりすぎないようにペナルティ項を追加して \begin{eqnarray} J_r(\boldsymbol{a}) = \sum_{n=0}^{N-1}\left\{ f(x_n,\boldsymbol{a}) - y_n \right\}^2 + \underbrace{\lambda ||\boldsymbol{a}||^2}_{ペナルティ項} \end{eqnarray} とし、通常の多項式回帰と同様に \begin{eqnarray} \frac{\partial J_r(\boldsymbol{a})}{\partial \boldsymbol{a}} &=& \boldsymbol{0} \end{eqnarray} から \begin{eqnarray} \left(\boldsymbol{X}+\lambda \boldsymbol{I}\right) \boldsymbol{a} &=& \boldsymbol{Y} \\ \end{eqnarray} を解けば、多項式係数 \(\boldsymbol{a}=(a_0,a_1,a_2,\cdots a_M)^T\) が求まります。なお、\(\lambda\) はペナルティの大きさを調節する正の定数です。
問題点
多項式は \begin{eqnarray} f(x,\boldsymbol{a}) &=& \sum_{m=0}^M a_m x^m\ =\ a_0 + a_1 x + a_2 x^2 + a_3 x^3 + \cdots a_M x^M \end{eqnarray}
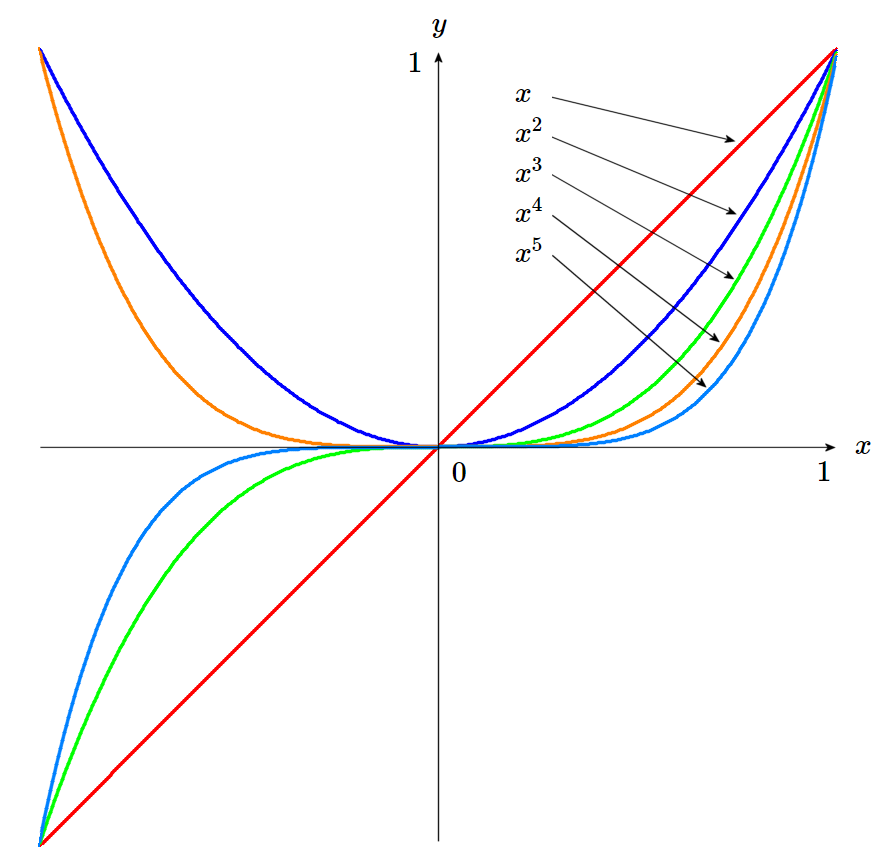
図1 : \(m\) が大きいほど \(x=0\) 付近で \(x^m\simeq 0\)
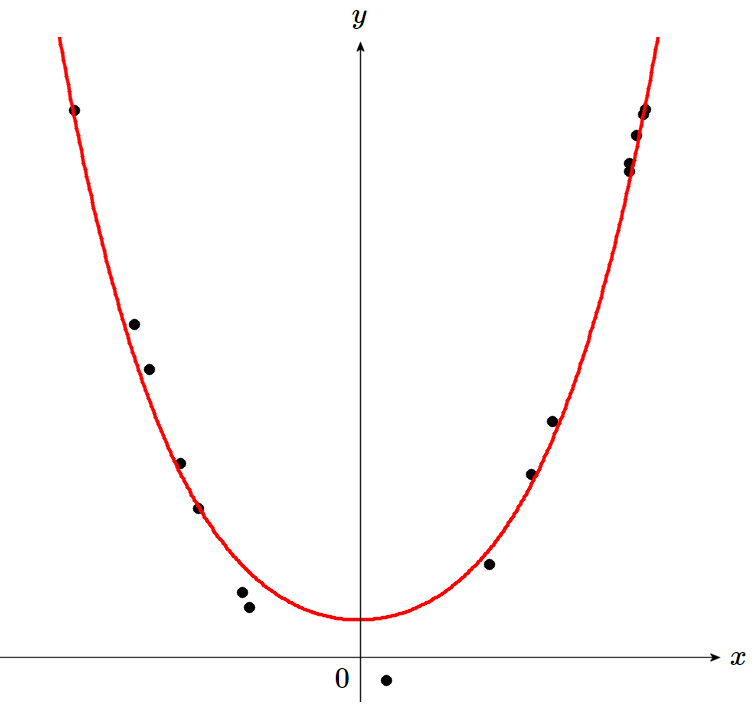
図2 : 多項式をリッジ回帰すると \(x=0\) 付近の精度が悪い
対策
\(x\simeq 0\) の時、\(x^m\simeq 0\) に潰れてしまうのが原因ですから、\(x_n\) に適当なオフセット \(d\) を加えて \(x_n' = x_n+d\) としたものを近似し、すべての \(x_n'\) を 0 から十分離してやれば、問題を回避できます。 \begin{eqnarray} f(x',\boldsymbol{a}) &=& \sum_{m=0}^M a_m (x+d)^m\ =\ a_0 + a_1 (x+d) + a_2 (x+d)^2 + a_3 (x+d)^3 + \cdots a_M (x+d)^M \end{eqnarray} ただし \(d\) が大きすぎると情報落ちによって精度が劣化してしまい、\(d\) が小さすぎると精度が悪い範囲が移動するだけで効果がありませんので、トレードオフが必要です。
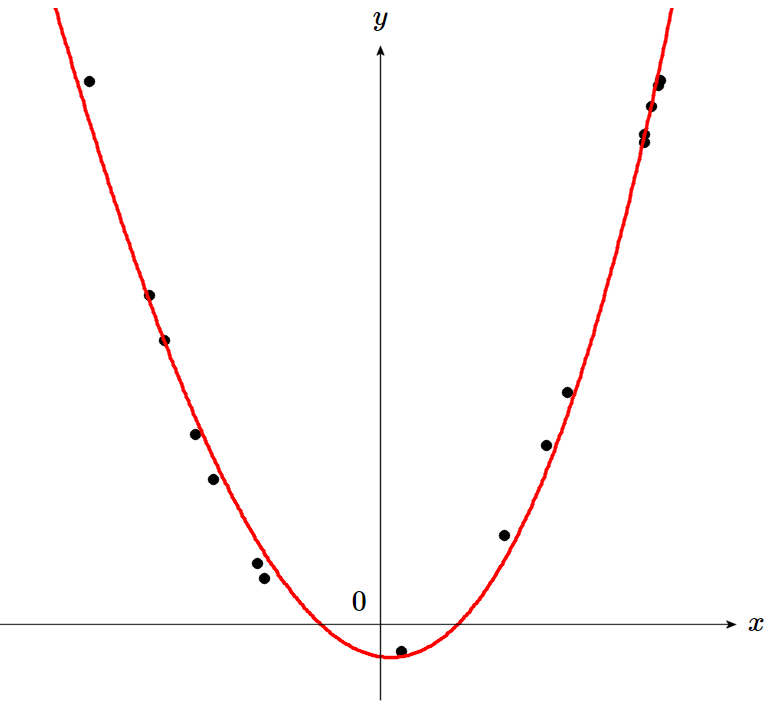
図3 : \(x_n' = x_n+d\) とシフトしてからリッジ回帰すると精度を確保できる